1. Activation Functions
Activation Functions 즉, 활성화 함수는 뉴런(노드)의 최종 값을 제공한다. input 데이터를 특정 범위의 출력으로 변환하는 단순한 함수이다.
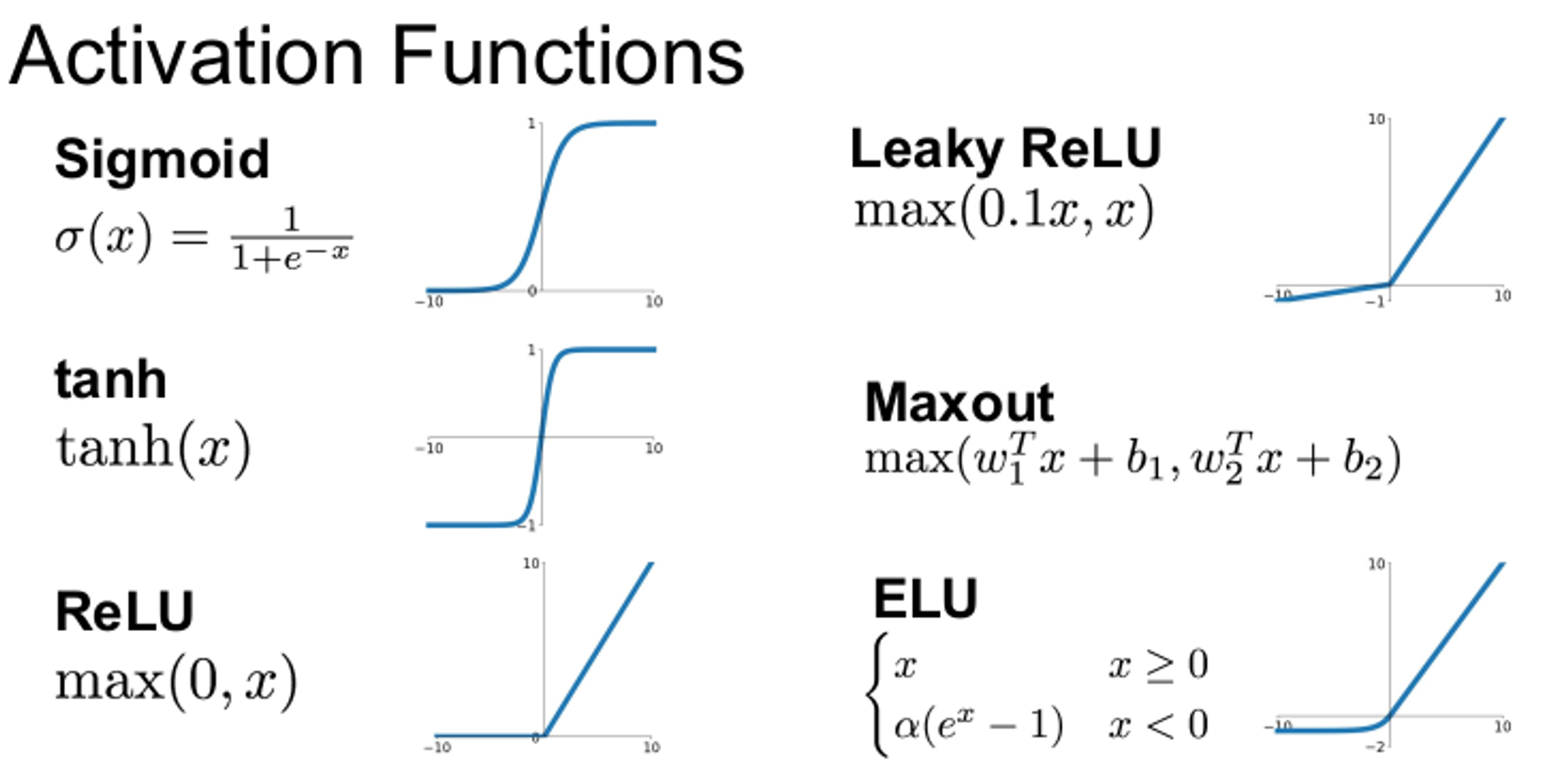
활성화 함수의 종류는 위와 같이 다양하다. 활성화 함수는 모두 비선형 함수이다.
1.1 Sigmoid 함수

Sigmoid 함수는 넓은 범위의 값을 [0,1] 사이의 값으로 만든다. 입력 값이 크면 1, 작으면 0에 가까워 진다. 0과 1 사이의 값은 선형 함수와 같은 모양이다.
하지만 Sigmoid 함수에는 3가지 문제점이 있다.
- Vanishing gradient
- x가 -10, 10일 경우엔 gradients가 0이다.
- Chain rule에 의해 gradient를 구할 때 곱연산을 지속적으로 하면 gradient는 점점 0에 가까워 진다.
- 0에 가까운 값에서만 sigmoid가 활성화 된다고 볼 수 있다.
- x의 값이 크거나 작은 경우에는 local gradient 값이 0이 되어 gradient가 없어지는 back propagation이 stop되는 결과가 나타나게 된다.
- Not zero-centered
- Sigmoid 함수의 출력값이 0을 중심으로 하지 않는다.
- Sigmoid 함수를 거친 값은 항상 양수의 값을 갖는다. backpropagation을 할 때 $W$가 같은 방향으로만 움직이기 때문에 parameter update를 할 때 다같이 증가하거나 감소한다. 이러한 업데이트는 비효율적이다.

3. Compute expensive
- exp() 는 연산이 커, 성능이 저하될 수 있다.
1.2 tanh 함수

tanh 함수는 [-1,1] 사이의 값을 갖기 때문에 Sigmoid 보다는 좋은 성능을 갖지만 여전히 vanishing gradient의 문제점을 갖고 있다.
1.3 ReLU 함수
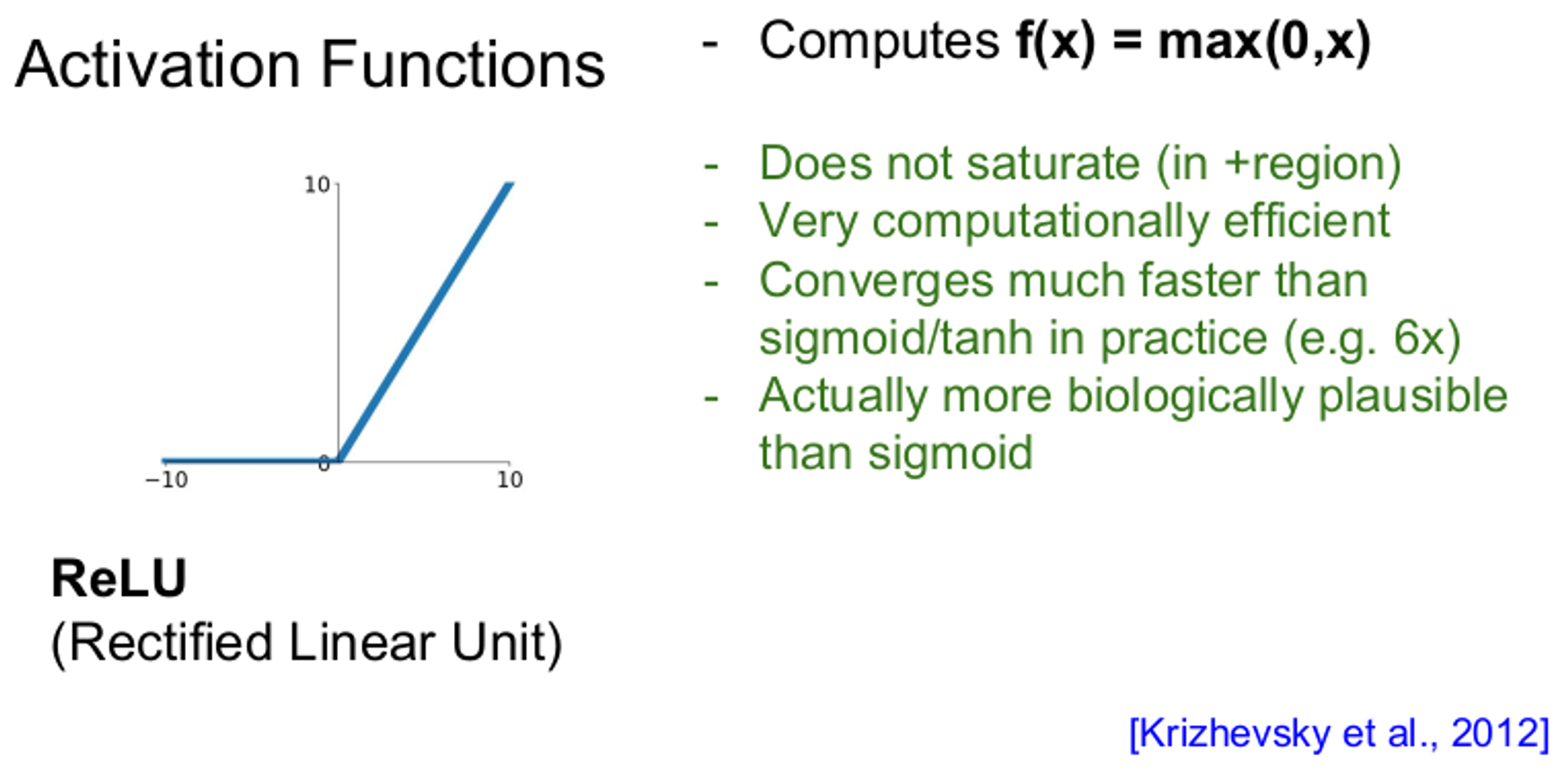
ReLU함수는 앞선 두 함수의 문제점을 해결한다. ReLU 함수는 양수일 때 뉴런이 포화되지 않아 gradient가 죽지 않으며, 계산이 효율적이다. 그러나 x < 0 일 때 gradient가 죽는다는 단점이 있다.
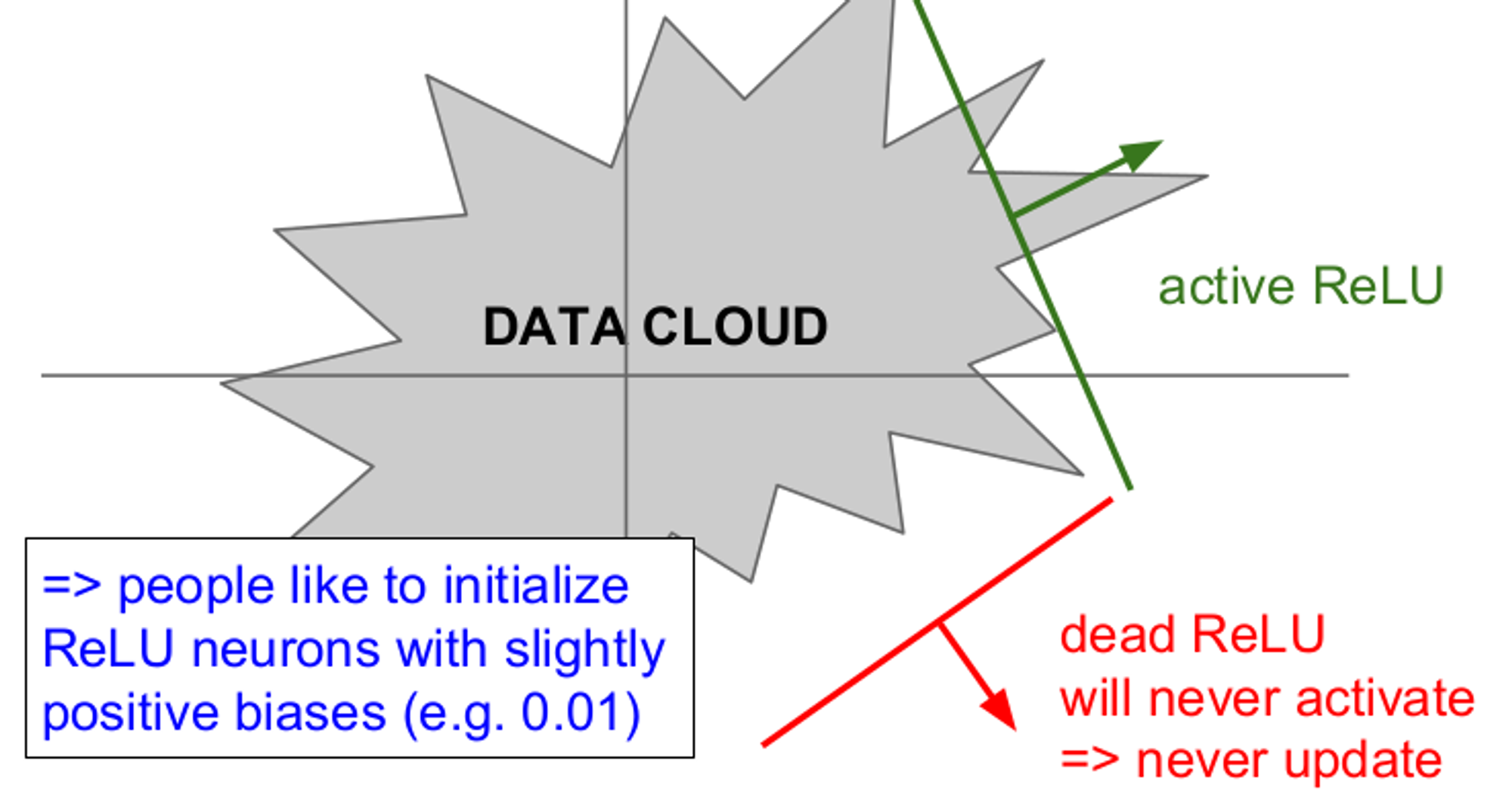
위 그림은 gradient를 절반만 죽이는 dead ReLU 현상을 설명한다. Data Cloud는 training data이며 dead ReLU에서는 활성화(active)가 일어나지 않고 업데이트 되지 않는다. 반면 active ReLU 에서는 일부는 활성화(active)되고 일부는 되지 않는다.
dead ReLU는 두 가지 경우에 발생한다.
- 가중치의 초기화가 잘못되어 가중치 평면이 Data Cloud와 멀리 떨어져 있을 때 발생한다.
- ReLU가 절대 활성화(active) 되지 않고 gradient가 업데이트 되지 않는다.
- learning rate가 너무 클 때 이다.
- learning rate가 너무 크면 처음에는 적절한 ReLU로 시작해도 업데이트가 너무 크게되어 ReLU가 Data Cloud에서 벗어나 버린다. 따라서 처음에는 잘 학습되다가 갑자기 죽어버리기도 한다. 실제로 ReLU를 사용하면 10~20%는 dead ReLU가 되는데 이는 크게 영향을 미치지 않는다.
이 밖에도 Leaky ReLU, ELU, Maxout ReLU의 변형된 형태의 활성화 함수가 있으며 강의에서는 ReLU를 learning rate에 유의하여 사용하며, sigmoid는 사용하지 않는 것이 좋으며, tanh함수는 사용하되 기대하지 말라고 언급하고 있다.
2. Data Preprocessing
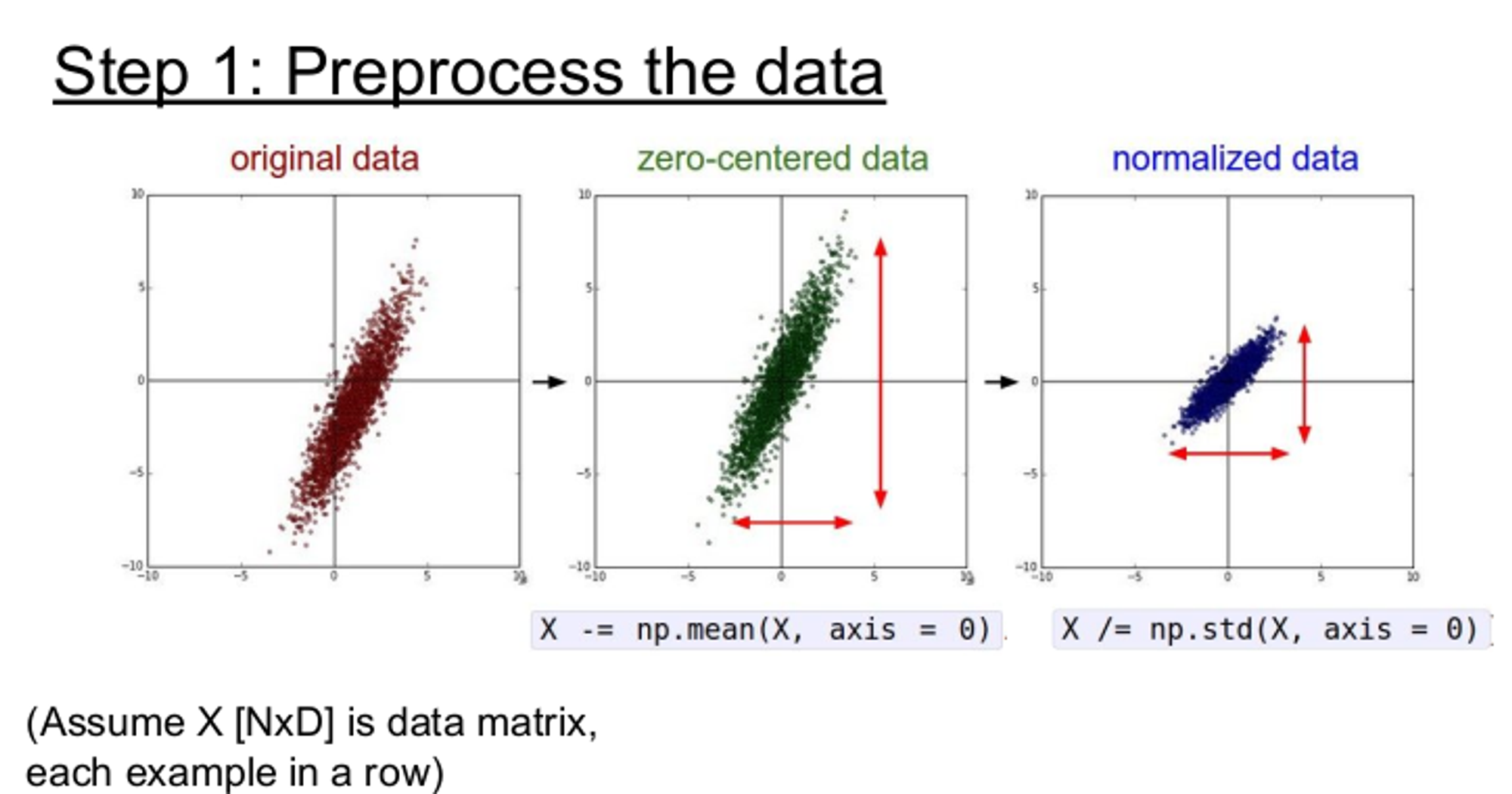
데이터의 전처리 방법은 위 그림과 같이 zero-centered data(데이터를 전체의 평균값으로 빼줌)으로 만들거나, normalized data(정규화)를 하는 방법이 있다.
zero-centered data로 만드는 이유는 입력이 모두 양수/음수인 경우는 모든 뉴런이 양수/음수인 gradient를 얻기 때문이다. 또한 normalized data로 만드는 이유는 모든 차원이 동일한 범위 안에 있게 하여 전부 동등한 기여를 하게 하기 위함이다. 이 외에도 PCA, Whitening 방법이 있지만 통계적 학습에 적합하므로 잘 사용하지 않는다.
3. Weight Initializing
가중치(W)가 0이 된다면 모든 parameter는 동일한 값으로 업데이트 되기 때문에 찾고자 하는 값을 찾기 어렵다. 따라서 Weight Initializing 즉, 가중치 초기화가 중요하다.
Small random numbers
아주 작은 임의의 숫자로 초기화 시키는 방법이다. 아주 작은 숫자로 초기화 시키기 때문에 어떤 활성화 함수를 쓰더라도 매우 작은 값들만 통과되며 깊은 신경망일수록 뒤쪽 layer에는 0에 가까운 input이 들어온다. back propagation에서 gradient가 사라진다는 점과, 학습하는데 굉장히 많은 시간이 소요된다는 단점이 있다. 표준편차에 따라 gradient 소실이 발생하지 않을 수 있지만 모든 함수의 출력값이 비슷해져 노드를 여러개 구성하는 의미가 사라진다.
Xavier
신경망이 tanh 또는 sigmoid를 활성화 하면 가중치 초기화를 위해 Xavier initializing을 할 수 있다. 단순히 표준편차를 줄이는 방식이 아닌 출력값들이 Gaussian 분포 형태를 가질 수 있게 만들어주는 방법이다. 표준편차를 이전 은닉층의 노드 수에 맞추어 변화시킨다. 이전 은닉층의 노드의 개수가 n개 이고 현재 은닉층의 노드가 m개일 때, $\frac{2}{\sqrt{n+m}}$을 표준편차로 하는 정규분포로 가중치를 초기화 한다. 고정 값을 곱해서 W를 주는 것보다 상대적으로 입력값의 개수에 따라 상대적으로 값을 조절하여 초기화를 해준다. Xavier initializing을 사용하면 hidden layer의 출력값이 Gaussian 형태를 갖게 된다.
He
ReLU 함수를 활성화 함수로 사용할 때 추천되는 초기화 방법이다. 해당 출력의 분산을 대략 1로 만들기 위해 선택할 수 있는 방법 중 하나이다.
요약
활성화 함수에 따라 적절한 초기화 방법이 달라진다. 일반적으로 활성화 함수가 Sigmoid 함수일 때는 Xavier 초기화를 ReLU류 함수일 때는 He 초기화를 사용한다.
4. Batch Normalization
평균과 분산을 조정하는 과정이 별도의 과정으로 떼어진 것이 아니라, 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정 역시 같이 조절된다. 즉, 레이어마다 정규화 하는 레이어를 두어, 변형된 분포가 나오지 않도록 조절하게 하는 것이다.

배치 정규화는 미니배치의 평균과 분산을 이용해 정규화 한 뒤, scale and shift를 감마(γ), 베타(β)값을 통해 실행한다. 이 때 감마(γ), 베타(β)는 학습 가능한 변수이다. 즉, Backpropagation을 통해서 학습된다.
mini-batch마다 mean, variance를 계산하고 구한 mean, variance로 normalize를 해준다. batch normalization은 scailing과 shifting factor를 갖고 있다. batch normalization은 기울기의 흐름에 좋은 영향을 주어 더욱 robust한 결과를 이끌어내고, learning rate의 범위를 더욱 확장시켜 더 많은 initialization을 유도할 수 있게 한다.
5. Hyperparameter Optimization
최적값이 존재하는 범위를 찾아가는 방법이다. 하이퍼파라미터 값을 Cross-validation stategy, Random search, Grid search 등의 방법을 이용하여 골라낸(샘플링) 후 그 값으로 정확도를 평가하는 과정을 반복하며 최적값의 범위를 좁혀나가는 방법이다.
'Study > cs231n' 카테고리의 다른 글
| [cs231n] 7. Training Neural Networks 2 (0) | 2024.04.17 |
|---|---|
| [cs231n] 5. Convolutional Neural Networks (0) | 2024.04.17 |
| [cs231n] 4. Introduction graphs (0) | 2024.04.17 |
| [cs231n] Loss Functions and Optimization 요약 (0) | 2024.04.04 |
