Diffusion 꼭 알아야하는 방법론
Generic Framework
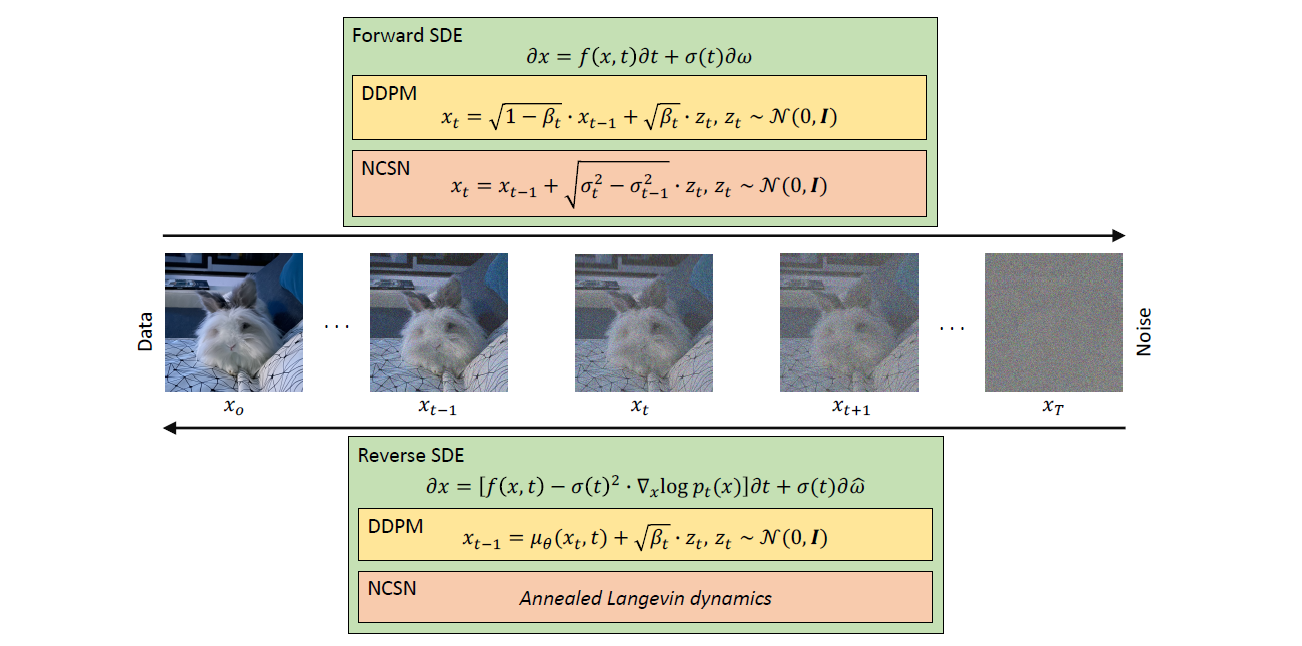
1. Denoising Diffusion Probabilistic Models (DDPMs)
Forward process
DDPM은 Gaussian noise를 통해 데이터를 망가뜨린다. $p(x_0)$ 가 data density라면 ($x_0$은 original data). 원본 $x_0$와 노이즈가 추가된 $x_1, x_2, ..., x_T$는 Markovian process를 거친다.
$$ p(x_t|x_{t-1}) = \mathcal{N}({x_t};\sqrt{1-\beta_t}\cdot x_{t-1}, \beta_t \cdot \mathbf{I}) $$
$T$는 diffusion steps를 의미하며, $\beta_1, beta_2, ..., \beta_T \in \lbrace 0,1)$는 diffusion steps의 variance schedule를 의미한다. $\mathbf{I}$ 는 input 이미지 $x_0$ 와 같은 차원을 갖는 identity matrix, $\mathbf{N}(x; \mu, \sigma)$ 는 평균 $\mu$, 분산 $\sigma$로 $x$를 생성해내는 정규분포를 뜻한다.
$p(x_t|x_0)$ 으로부터 샘플링하는 것은 reparametrization trick을 통해 가능하다. 일반적으로 표준화된 샘플 $x \sim \mathcal{N}(\mu, \sigma^2 \cdot \mathbf{I})$을 생성하기 위해 평균 $\mu$와 표준편차 $\sigma$ 를 통해 $z \sim \mathcal{N}(0,\mathbf{I})$를 사용한다. 이를 통해 각 step에서 생성된 이미지 $x_t$는 아래와 같다.
$$ x_t = \sqrt{\hat\beta_t} \cdot x_0 + \sqrt{(1-\hat \beta_t}) \cdot z_t $$
Properties of $\beta_t$
variance schedule $\beta^T_{t=1}$로 $\hat \beta_T \rightarrow 0$라면, $x_T$의 분포는 가우시안 분포에 잘 근사할 것이다. DDPM 논문의 경우, $T =1000$, $\beta_1 = 10^{-4}$ 와 $\beta_T = 2 \cdot 10^{-2}$으로 정의하였다.
Reverse process
$p(x_0)$로 부터 새로운 샘플을 생성할 수 있다. 샘플 $x_T \sim \mathcal{N}(0, \mathbf{I})$ 및 reverse steps $(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu(x_t,t), \sum_\theta(x_t,t))$을 따른다. 이러한 step에 근사하기 위해 신경망을 다음과 같이 학습시킬 수 있다.
$$ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t,t), \sum_\theta(x_t,t)) $$
노이즈가 추가된 이미지 $x_t$와 time step embedding $t$로 부터 평균 $\mu_\theta(x_t,t)$와 공분산 $\sum_\theta(x_t,t)$를 학습할 수 있다.
이상적으로는 신경망을 Maximum Likelihood 목적식을 통해 학습하는거지만 현실적으로 불가능하기 때문에 negative log-likelihood의 Variational lower-bound를 최소화하여 학습한다.
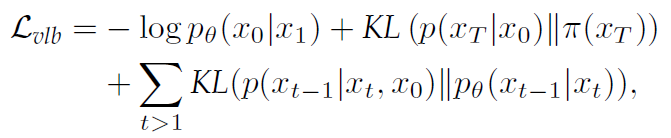
KL 은 두 분포간의 Kullback-Leibler divergence 를 의미한다. 위 식에서 두 번째 항의 경우에는 $\theta$에 영향을 받지 않기 때문에 배제할 수 있고, 마지막 항의 경우엔 각 time step $t$에서 $p_\theta(x_{t-1}|x_t)$ true posterior의 분포에 가깝게 추정되도록 한다.
이는 사후확률 $p(x_{t-1}|x_t,x_0)$이 가우시안 분포를 따른다는 것을 통해 증명할 수 있다.

DDPM 논문에서는 covariance $\sum_\theta(x_t,t)$를 고정하여 평균 $\mu_\theta(x_t,t$ 만 학습하도록 아래와 같이 정의하였다.
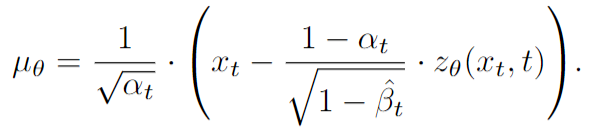
이를 통해 loss를 variational lower bound가 아닌 단순한 MSE 형태로 구할 수 있게 하였다.
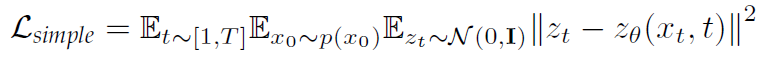
생성 프로세스는 모델이 각 이미지에서 노이즈를 예측하게 하고, 평균은 앞의 앞에 식에서 정의한다.
2. Noise Conditioned Score Networks(NCSNs)
데이터 밀도 $p(x)$는 로그 밀도 함수 $\nabla_x \space log \space p(x)$의 기울기에 의해 정의된다. 이 기울기의 방향은 Langevin dynamics 알고리즘이 사용된다. [Langevin dynamics] 는 물리학에서 나온 iterative method로 데이터 샘플링에 적용할 수 있는 방법이다.
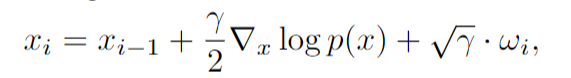
$\gamma$는 score의 direction을 조절하는데 사용되며, $x_0$는 사전확률(prior)분포로 부터 생성되고, 노이즈 $w_i \sim \mathcal{N}(0,\mathbf{I})$는 local minima에 빠지는 것을 방지한다. 따라서 생성모델은 $p(x)$를 신경망 $s_\theta(x) \approx \nabla_x \space log \space p(x)$
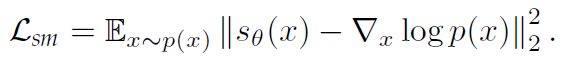
$ \nabla_x \space log \space p(x)$가 알 수 없기 때문에 위 목적식을 최소화하는 것은 불가능하다. 따라서 denoising score matching & sliced score matching 을 사용하여 극복한다.
이를 실제 데이터에 적용하면 여러가지 문제들이 발생하는데 대부분의 문제는 manifold 가정과 관련이 있다. 그런 문제를 보완하기 위해 NCSN(Noise Conditioned Scored Network)를 통해 노이즈 분포에 대한 score 추정치를 학습할 것을 제안한다. 샘플링과 관련해 Langevin dynamics를 적용하여 score를 추정한다.
Gaussian noise가 sequential하게 주어지면 ($\sigma_1 < \sigma_2 < \cdot \cdot \cdot < \sigma_T$) denoising score mathcing을 통해 NCSN $s_\theta (x, \sigma_t)$를 학습해 $s_\theta(x, \sigma_t) \approx \nabla_x \space log \space (p_{\sigma_t}(x))$를 얻을 수 있다.
$ \nabla_x \space log \space (p_{\sigma_t}(x))$는 아래와 같이 정의할 수 있다.
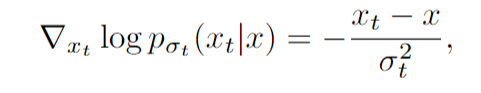
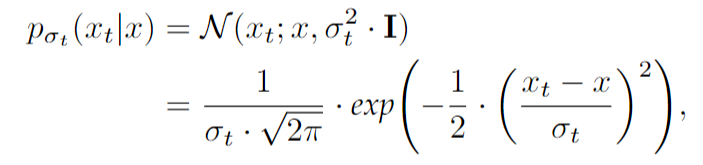
$x_t$는 $x$의 노이즈가 끼어있는 형태이다. 정리하면, 위 $\mathcal{L}_{sm}$을 모든 $(\sigma_t{{t=1}^T} $ 에 대해서 생성하고 기울기를 차례대로 바꿔 나가는 것은 $s_\theta(x_t, \sigma_t)$를 아래 목적식에 따라 학습하는 것이다.
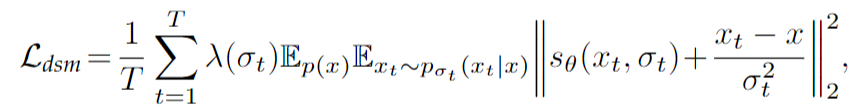
학습 후에는 noisy image $x_t$와 time step $t$가 신경망 $s_\theta(x_t, \sigma_t)$을 통해 score $\nabla_{x_t} \space log \space (p_{\sigma_t}(x_t))$의 추정값을 얻을 수 있다.

3. Stochastic Differential Equations (SDEs)
앞 선 두 가지 방법론과 마찬가지로 데이터 분포 $p(x_0)$을 노이즈로 변환한다. reverse process는 각 time step에서 density의 score function을 필요로 하는 reverse-time SDE를 모델링할 수 있다. [Score-Based Generative Modeling through Stochastic Differential Equation]에서는 신경망을 사용해 score function을 추정하고, numeric SDE solver를 사용해 $p(x_0)$에서 샘플을 생성한다. 앞서 NCSN와 마찬가지로 신경망은 perturbed data와 time step을 입력으로 하고 score function의 추정치를 생성한다.
SDE의 forward diffusion process는 아래와 같다.
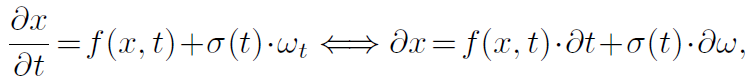
$w_t$는 Gaussian noise이며, $f$는 $x$와 $t$에 대한 drift coefficient를 계산하는 함수이다. $\sigma$는 Diffusion coefficient를 계산하는 시간 의존성 함수이다. SDE에 대한 솔루션으로 Diffusion process를 사용하려면 데이터 $x_0$을 점진적으로 무효화하고 diffusion coefficient가 가우스 노이즈의 추가량을 제어하도록 drifit coefficient를 설계해야 한다. SDE는 아래와 같이 정의된다.
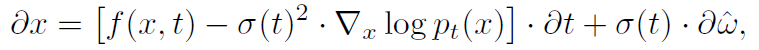
$\hat w$는 reverse time($T \rightarrow 0$)에서 Brownian motion을 표현한다. reverse-time SDE는 pure한 noise로부터 drift를 제거하여 데이터를 복원하게 된다. 신경망 $s_\theta(x,t) \approx \nabla_x \space log \space p_t(x) $ 를 학습한다. 앞서 나온 목적식과 동일하지만 continuous 할 때라는 점에서 차이가 있다.
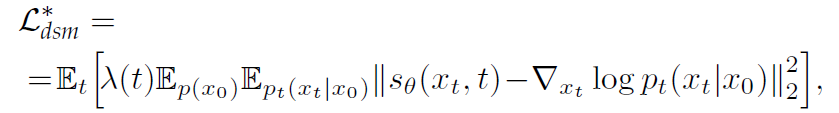
$\lambda$는 weighting function, $t \sim \mathcal{U}([0,T])$ 이다. drift coefficient $f$는 affine이며, $p_t(x_t|x_0)$은 가우시안 분포이다.
이 접근법에 대한 샘플링은 SDE에 적용된 numerical method로 수행할 수 있다. solver는 continuous 식에서는 작동하지 않는다.
[Score-Based Generative Modeling through Stochastic Differential Equation] 논문에서는 샘플링 부분에서 몇 가지 contribution이 있다. Predictor-Corrector sampler를 통해 더 나은 샘플을 생성해낸다. 먼저 reverse-time SDE에서 샘플링하기 위해 numerical method를 사용한 다음, score based method를 corrector로 사용한다. 예를 들어 Euler-Maruyama method는 작은 negative step $\Delta t$를 고정하고, 초기 time step $t=T$가 $t=0$이 될 때 까지 아래 알고리즘을 적용한다.

Reference
Croitoru, F. A., Hondru, V., Ionescu, R. T., & Shah, M. (2023). Diffusion models in vision: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence.
'Study > Paper' 카테고리의 다른 글
Diffusion 꼭 알아야하는 방법론
Generic Framework

1. Denoising Diffusion Probabilistic Models (DDPMs)
Forward process
DDPM은 Gaussian noise를 통해 데이터를 망가뜨린다. $p(x_0)$ 가 data density라면 ($x_0$은 original data). 원본 $x_0$와 노이즈가 추가된 $x_1, x_2, ..., x_T$는 Markovian process를 거친다.
$$ p(x_t|x_{t-1}) = \mathcal{N}({x_t};\sqrt{1-\beta_t}\cdot x_{t-1}, \beta_t \cdot \mathbf{I}) $$
$T$는 diffusion steps를 의미하며, $\beta_1, beta_2, ..., \beta_T \in \lbrace 0,1)$는 diffusion steps의 variance schedule를 의미한다. $\mathbf{I}$ 는 input 이미지 $x_0$ 와 같은 차원을 갖는 identity matrix, $\mathbf{N}(x; \mu, \sigma)$ 는 평균 $\mu$, 분산 $\sigma$로 $x$를 생성해내는 정규분포를 뜻한다.
$p(x_t|x_0)$ 으로부터 샘플링하는 것은 reparametrization trick을 통해 가능하다. 일반적으로 표준화된 샘플 $x \sim \mathcal{N}(\mu, \sigma^2 \cdot \mathbf{I})$을 생성하기 위해 평균 $\mu$와 표준편차 $\sigma$ 를 통해 $z \sim \mathcal{N}(0,\mathbf{I})$를 사용한다. 이를 통해 각 step에서 생성된 이미지 $x_t$는 아래와 같다.
$$ x_t = \sqrt{\hat\beta_t} \cdot x_0 + \sqrt{(1-\hat \beta_t}) \cdot z_t $$
Properties of $\beta_t$
variance schedule $\beta^T_{t=1}$로 $\hat \beta_T \rightarrow 0$라면, $x_T$의 분포는 가우시안 분포에 잘 근사할 것이다. DDPM 논문의 경우, $T =1000$, $\beta_1 = 10^{-4}$ 와 $\beta_T = 2 \cdot 10^{-2}$으로 정의하였다.
Reverse process
$p(x_0)$로 부터 새로운 샘플을 생성할 수 있다. 샘플 $x_T \sim \mathcal{N}(0, \mathbf{I})$ 및 reverse steps $(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu(x_t,t), \sum_\theta(x_t,t))$을 따른다. 이러한 step에 근사하기 위해 신경망을 다음과 같이 학습시킬 수 있다.
$$ p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t,t), \sum_\theta(x_t,t)) $$
노이즈가 추가된 이미지 $x_t$와 time step embedding $t$로 부터 평균 $\mu_\theta(x_t,t)$와 공분산 $\sum_\theta(x_t,t)$를 학습할 수 있다.
이상적으로는 신경망을 Maximum Likelihood 목적식을 통해 학습하는거지만 현실적으로 불가능하기 때문에 negative log-likelihood의 Variational lower-bound를 최소화하여 학습한다.
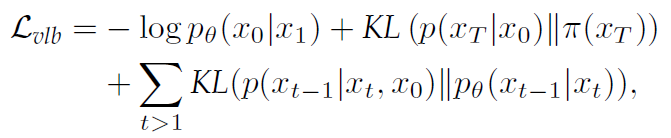
KL 은 두 분포간의 Kullback-Leibler divergence 를 의미한다. 위 식에서 두 번째 항의 경우에는 $\theta$에 영향을 받지 않기 때문에 배제할 수 있고, 마지막 항의 경우엔 각 time step $t$에서 $p_\theta(x_{t-1}|x_t)$ true posterior의 분포에 가깝게 추정되도록 한다.
이는 사후확률 $p(x_{t-1}|x_t,x_0)$이 가우시안 분포를 따른다는 것을 통해 증명할 수 있다.

DDPM 논문에서는 covariance $\sum_\theta(x_t,t)$를 고정하여 평균 $\mu_\theta(x_t,t$ 만 학습하도록 아래와 같이 정의하였다.
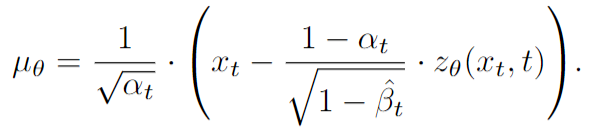
이를 통해 loss를 variational lower bound가 아닌 단순한 MSE 형태로 구할 수 있게 하였다.
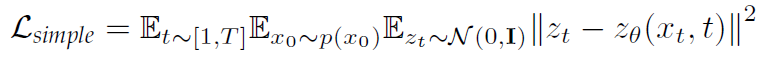
생성 프로세스는 모델이 각 이미지에서 노이즈를 예측하게 하고, 평균은 앞의 앞에 식에서 정의한다.
2. Noise Conditioned Score Networks(NCSNs)
데이터 밀도 $p(x)$는 로그 밀도 함수 $\nabla_x \space log \space p(x)$의 기울기에 의해 정의된다. 이 기울기의 방향은 Langevin dynamics 알고리즘이 사용된다. [Langevin dynamics] 는 물리학에서 나온 iterative method로 데이터 샘플링에 적용할 수 있는 방법이다.
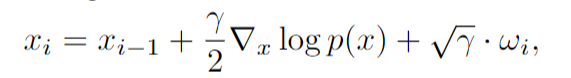
$\gamma$는 score의 direction을 조절하는데 사용되며, $x_0$는 사전확률(prior)분포로 부터 생성되고, 노이즈 $w_i \sim \mathcal{N}(0,\mathbf{I})$는 local minima에 빠지는 것을 방지한다. 따라서 생성모델은 $p(x)$를 신경망 $s_\theta(x) \approx \nabla_x \space log \space p(x)$
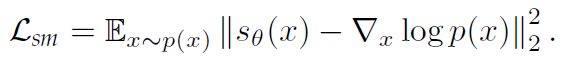
$ \nabla_x \space log \space p(x)$가 알 수 없기 때문에 위 목적식을 최소화하는 것은 불가능하다. 따라서 denoising score matching & sliced score matching 을 사용하여 극복한다.
이를 실제 데이터에 적용하면 여러가지 문제들이 발생하는데 대부분의 문제는 manifold 가정과 관련이 있다. 그런 문제를 보완하기 위해 NCSN(Noise Conditioned Scored Network)를 통해 노이즈 분포에 대한 score 추정치를 학습할 것을 제안한다. 샘플링과 관련해 Langevin dynamics를 적용하여 score를 추정한다.
Gaussian noise가 sequential하게 주어지면 ($\sigma_1 < \sigma_2 < \cdot \cdot \cdot < \sigma_T$) denoising score mathcing을 통해 NCSN $s_\theta (x, \sigma_t)$를 학습해 $s_\theta(x, \sigma_t) \approx \nabla_x \space log \space (p_{\sigma_t}(x))$를 얻을 수 있다.
$ \nabla_x \space log \space (p_{\sigma_t}(x))$는 아래와 같이 정의할 수 있다.
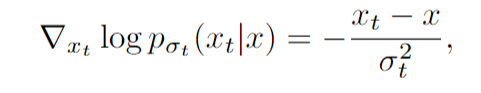
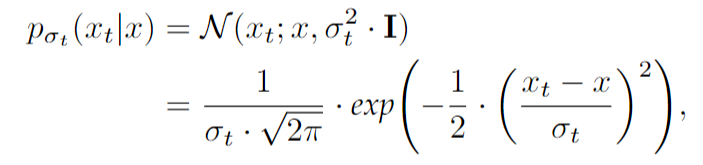
$x_t$는 $x$의 노이즈가 끼어있는 형태이다. 정리하면, 위 $\mathcal{L}_{sm}$을 모든 $(\sigma_t{{t=1}^T} $ 에 대해서 생성하고 기울기를 차례대로 바꿔 나가는 것은 $s_\theta(x_t, \sigma_t)$를 아래 목적식에 따라 학습하는 것이다.
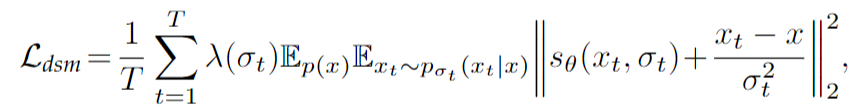
학습 후에는 noisy image $x_t$와 time step $t$가 신경망 $s_\theta(x_t, \sigma_t)$을 통해 score $\nabla_{x_t} \space log \space (p_{\sigma_t}(x_t))$의 추정값을 얻을 수 있다.

3. Stochastic Differential Equations (SDEs)
앞 선 두 가지 방법론과 마찬가지로 데이터 분포 $p(x_0)$을 노이즈로 변환한다. reverse process는 각 time step에서 density의 score function을 필요로 하는 reverse-time SDE를 모델링할 수 있다. [Score-Based Generative Modeling through Stochastic Differential Equation]에서는 신경망을 사용해 score function을 추정하고, numeric SDE solver를 사용해 $p(x_0)$에서 샘플을 생성한다. 앞서 NCSN와 마찬가지로 신경망은 perturbed data와 time step을 입력으로 하고 score function의 추정치를 생성한다.
SDE의 forward diffusion process는 아래와 같다.
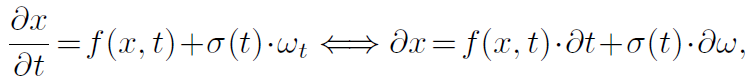
$w_t$는 Gaussian noise이며, $f$는 $x$와 $t$에 대한 drift coefficient를 계산하는 함수이다. $\sigma$는 Diffusion coefficient를 계산하는 시간 의존성 함수이다. SDE에 대한 솔루션으로 Diffusion process를 사용하려면 데이터 $x_0$을 점진적으로 무효화하고 diffusion coefficient가 가우스 노이즈의 추가량을 제어하도록 drifit coefficient를 설계해야 한다. SDE는 아래와 같이 정의된다.
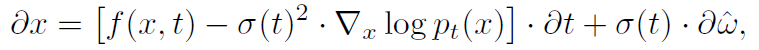
$\hat w$는 reverse time($T \rightarrow 0$)에서 Brownian motion을 표현한다. reverse-time SDE는 pure한 noise로부터 drift를 제거하여 데이터를 복원하게 된다. 신경망 $s_\theta(x,t) \approx \nabla_x \space log \space p_t(x) $ 를 학습한다. 앞서 나온 목적식과 동일하지만 continuous 할 때라는 점에서 차이가 있다.
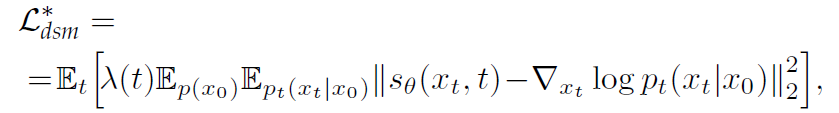
$\lambda$는 weighting function, $t \sim \mathcal{U}([0,T])$ 이다. drift coefficient $f$는 affine이며, $p_t(x_t|x_0)$은 가우시안 분포이다.
이 접근법에 대한 샘플링은 SDE에 적용된 numerical method로 수행할 수 있다. solver는 continuous 식에서는 작동하지 않는다.
[Score-Based Generative Modeling through Stochastic Differential Equation] 논문에서는 샘플링 부분에서 몇 가지 contribution이 있다. Predictor-Corrector sampler를 통해 더 나은 샘플을 생성해낸다. 먼저 reverse-time SDE에서 샘플링하기 위해 numerical method를 사용한 다음, score based method를 corrector로 사용한다. 예를 들어 Euler-Maruyama method는 작은 negative step $\Delta t$를 고정하고, 초기 time step $t=T$가 $t=0$이 될 때 까지 아래 알고리즘을 적용한다.

Reference
Croitoru, F. A., Hondru, V., Ionescu, R. T., & Shah, M. (2023). Diffusion models in vision: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence.
